
Optics
Learning physics
and chemistry
easily and freely - Science for elementary school, middle school and
high school
Free online optic lesson for elementary school, middle school and high school.
Propagation of light
Beams of light
1) What is a beam of light ?
Generally, a light source emits light in in several directions: All the rays of light then correspond to a light beam.
A beam of light can be represented by drawing its upper and lower ray of light.
Example: Beam of light from a flashlight
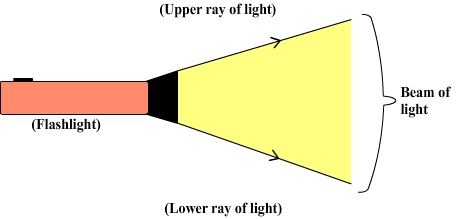
2) Can we see a beam of light ?
When a screen is lighted by a flashlight, we can see a spot of light on this screen because it diffuses (like other secondary sources) the received light. Nevertheless the beam of light between the flashlight and the screen can't be seen.
Light emitted by a ( primary or secondary ) source enables to see this source but light emitted can't be seen.
However, we can visualize a beam of light with particles (dust, smoke or even drop of water) that behave as diffusing objects when located within the beam of light

| Science class |
| Optics lessons |
Light sources - Types of light sources - Why can we see objects ? Propagation of light - Rectilinear propagation of light - Beams of light - Speed of light - Light and distances Shadows, lunar eclipses and phases of the moon - Formation of shadows - The Moon and eclipses Colored lights - color of objects - Decomposition of white light - Colored lights - Color of objects Image formation - Thin lenses - Thin converging and diverging lenses - Image formation by thin lenses - Vision and eyes |
|
|
©2021 Physics and chemistry


